Hyperspectral Image Fusion

Hyperspectral imaging (HSI) collects several images (bands) over a wide and continuous wavelength range. This forms a hyperspectral (HS) cube formed by 3 dimensions — 2 for the spatial position and 1 for the spectral coordinate ($x,y,\lambda$). 1

HSI has proven its usefulness with its rich spectral information, but lacks acutely in terms of spatial resolution. This is caused by hardware limitations — a long exposure is necessary to collect enough photons while maintaining a good signal-to-noise ratio, leading to low spatial resolutions. 2

The lack of spatial resolution hinders the development of further HSI applications and diminishes the accuracy of the already existing ones. Nevertheless, the hardware limitations can be overcome with software-based approaches to improve the resolution of hyperspectral images.

These approaches are named Hyperspectral Super Resolution methods (HSSR). These methods which improve the spatial resolution of hyperspectral images: (1) improves the applicability of this technology across all the pre-existing applications, and (2) allows for other novel usages that would otherwise not have been possible with the available low-resolution HS images.

This text is focused on Hyperspectral Image Fusion (HIF) which is a sub-tupe of HSSR. The goal of HIF is to obtain an accurate super-resolution hyperspectral image from two input images: a low-spatial high-spectral resolution image and a high-spatial low-spectral resolution image.

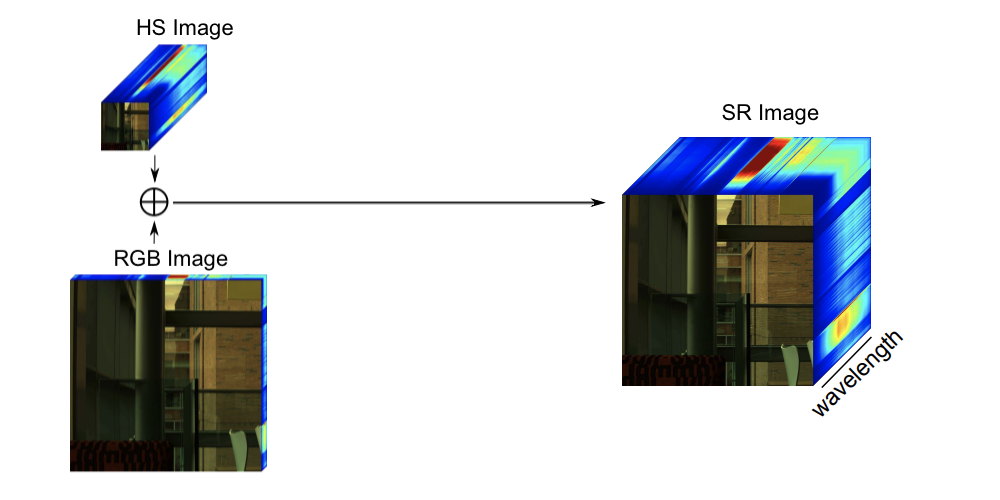
The image above can be described as follows: a HS cube contains the spectrum of light for each pixel and is formed by two dimensions that represent the spatial position ($x,y$), and a third that is the spectral coordinate ($\lambda$). Therefore, a cube $\mathbf{C}$ can be mathematically described as $\mathbf{C} \in \mathbb{R}^{x \times y \times \lambda}$.

Based on this convention, the inputs and corresponding output of the system can be formally summarized as follows. Let $\mathbf{HS} \in \mathbb{R}^{w \times h \times \Lambda}$ and $\mathbf{RGB} \in \mathbb{R}^{W \times H \times \lambda}$ be the two input images. The variables $w$, $h$ and $\lambda$ denote the width, the height and the spectral dimension respectively; with the same capital letters corresponding to the same variable but with high value, such that $W \gg w$, $H \gg h$ and $\Lambda \gg \lambda$. Additionally, $\lambda=3$ since the RGB image has three color channels RGB. From these inputs, we obtain the super-resolution hyperspectral image $\mathbf{SR} \in \mathbb{R}^{W \times H \times \Lambda}$ through

$\boldsymbol{\Psi}: \mathbb{R}^{w \times h \times \Lambda} \times \mathbb{R}^{W \times H \times 3} \rightarrow \mathbb{R}^{W \times H \times \Lambda}$

$\mathbf{SR} = \Psi(\mathbf{HS},\mathbf{RGB})$

Wald’s Protocol

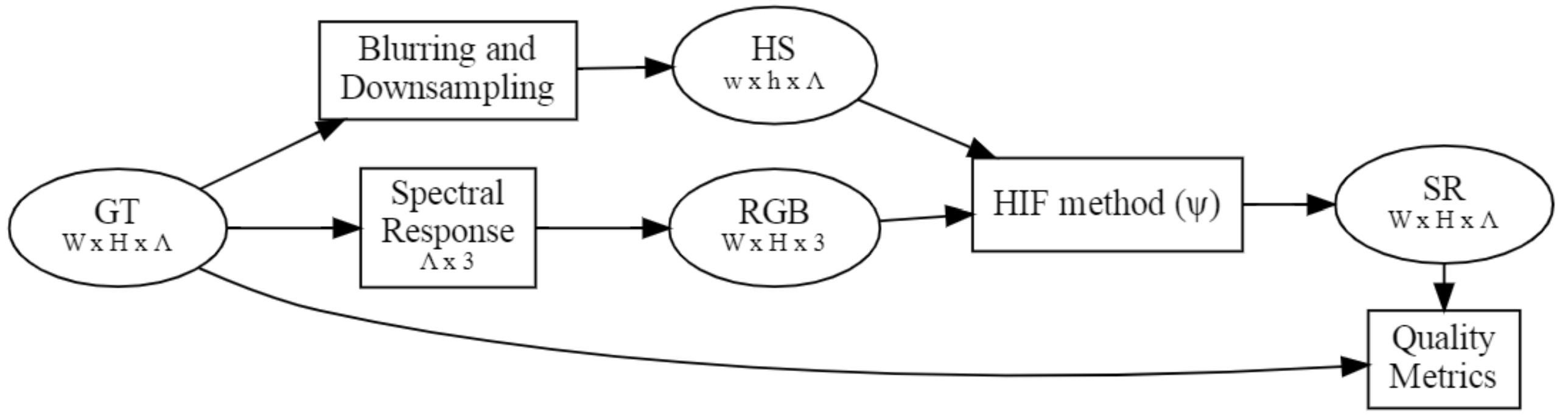
In 1997, Wald et. al. 3 proposed what would be named Wald’s Protocol, a paradigm for quality assessment of fused images, which can be described as follows:

  1. From the HS reference image, we produce two synthetic images that are going to be the input to the HIF method: (1) a low spatial resolution HS image, and (2) a high spatial resolution RGB image. To synthesize the low-spatial resolution hyperspectral image, the high-spatial resolution hyperspectral ground truth (GT) image is blurred and downsampled by a pre-defined scaling factor to a smaller spatial resolution; and to synthesize the RGB image we typically simulate a spectral response of an RGB camera over the GT image.
  2. Those two images serve as input to the HIF method that we are testing, which in turn produces a super-resolution (SR) HS image.
  3. The output SR HS image is then compared against the hyperspectral GT reference image. This is used to compute quality metrics and perform a visual analysis of the results.

To fully evaluate a HIF method it is necessary to have full-reference quality assessment metrics which ensure an objective comparison of the resolution enhancement process. These metrics can assess quality in the spectral domain (SAM and SID), in the spatial domain (SCC), or assess the global image quality (Total Error, RMSE, RASE, ERGAS, PSNR, SSIM, MS-SSIM, PSNR-B, UQI, VIF and Q2n).

If you are interested to learn more about the topic, please refer to my thesis titled “Hyperspectral Image Fusion: A Comprehensive review”, which contains a comprehensive review of the state-of-the-art of HIF. It includes a compilation of numerous HIF methods, tested with several image databases while measuring many quality metrics all at once, and in a generalized, fair, and extendable testing protocol.

Hyperspectral Image Fusion: A Comprehensive review

If you use any part of this work, please use the following citation:

Magalhães, Miguel. “Hyperspectral Image Fusion: A Comprehensive Review”. Master’s Programme in Imaging and Light in Extended Reality (IMLEX). MSc. thesis. KU Leuven, 2022.

@mastersthesis{hif_review_2022, title={Hyperspectral Image Fusion: A Comprehensive Review}, author={Miguel Magalhães}, year={2022}, school={KU Leuven}, note={Master’s Programme in Imaging and Light in Extended Reality (IMLEX)} }

  1. Manolakis, D., Marden, D., & Shaw, G. A. (2003). Hyperspectral image processing for automatic target detection applications. Lincoln laboratory journal, 14(1), 79-116. ↩︎

  2. Akhtar, N., Shafait, F., & Mian, A. (2014). Sparse spatio-spectral representation for hyperspectral image super-resolution. In Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part VII 13 (pp. 63-78). Springer International Publishing. ↩︎

  3. Wald, L., Ranchin, T., & Mangolini, M. (1997). Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogrammetric engineering and remote sensing, 63(6), 691-699. ↩︎